How to derive the vehicle speed from wheelspeed
Introduction
Multiple vehicle dynamic models are used to represent the motion of various types of vehicles. Fixposition offers two options for customers to input wheel speed data into the sensor accurately, optimizing fusion performance in near-ideal wheel scenarios (minimal slippage).
Option 1 - Configure the sensor’s web interface: Configure the “Configuration → Wheelspeed“ setting. Here, you can configure multiple wheel speeds, and the system will take a comprehensive approach to calculate vehicle speed based on
wheelspeed (speed of revolution or linear velocity of the wheel in the X-direction based on VRTK2 sensor frame)
heading angle
and extrinsic values
The sensor will directly estimate the heading with its GNSS-VIO fusion system without reading steering angle signals from the CAN directly. The default vehicle dynamic models supported are:
Balanced car model (lateral two-wheel model, e.g., two-wheel robot)
Bicycle model (longitudinal two-wheel model)
4WS (Four-wheel-distributed) vehicle model with front steering (e.g., four-wheel robot; SUV robot)
FWD (Front wheel drive) vehicle model with front steering (e.g., vehicle)
RWD (Rear wheel drive) vehicle model with front steering (e.g., vehicle)
In this option, you just need to focus on configuring the extrinsic between the VRTK2 and the wheelspeed sensor and data interface (TCP/UART/CAN) to stream in the signals of the wheelspeed sensor.
Right now, we focus on estimating velocity in the X-dimension temporarily.
Option 2 - Configure the Fixposition ROS driver (still need to configure the sensor’s web interface, but the data interface is TCP): Directly stream the vehicle speed in the X-directional instead of wheel speed into the Fixposition ROS driver; this velocity data will then be input into the VRTK2 sensor.
Recommend sending only component of velocity in the direction of movement rather than rear chassis wheel speed, which would help with the robustness of velocity estimation
Customers can calculate vehicle speed based on wheel speed and their dynamic models or use redundant sensor data resources to obtain vehicle speed and then project the values into X-axis, such as:
LiDAR data
millimeter-wave radar data
4D radar data
Optical ground speed sensor data
Reference:
TODO:
add some algorithm implementation reference here…
some paper reference here
Here are some common dynamic models, besides the ones mentioned above, that Fixposition customers may use to calculate vehicle speed:
RWD (Rear wheel drive) vehicle model with rear steering (e.g., large sweeper)
4WS (Four-wheel-distributed) vehicle model without a steering wheel (e.g., some robotic chassis)
Front-rear steering articulated vehicle (e.g., some tractors)
TOADD
Parameters, Basic Theory, Assumption
Vehicle speed is derived from longitudinal and lateral velocities. For different models, we will list the methods to calculate vehicle speed from wheel speed, wheel steering angle, and extrinsic parameters of the vehicle wheel with the mounted sensor.
Parameters
: longitudinal velocity,
: longitudinal velocity,
: vehicle velocity,
and
: angular speeds of the left and right wheels,
: the wheel radius,
: the distance between the front wheels (track width).
: the distance between the front and rear axles (wheelbase).
: vehicle steering angle or heading angle,
and
: the steering angles of the left and right wheels
and
: the steering angles of the front and rear axle if it is a four wheel steering system and both of their steering mechanism are based on the Ackermann steering geometry
: the steering angles of the front left, front right, rear left, rear right wheels respectively if it is a four wheel steering system
Ackermann steering principle
Cars use the Ackermann steering principle. The idea behind the Ackermann steering is that the inner wheel (closer to ICR) should steer for a bigger angle than the outer wheel in order to allow the vehicle to rotate around the middle point between the rear wheel axis.
Keep in mind that the above two values are considered based on the Ackermann steering principle.
The overall steering angle based on the Ackermann steering principle depends on the steering angles of the front wheels and the distance between the front and rear axles. The Ackermann steering principle ensures that the inside and outside wheels follow different turning radii to minimize tire scrubbing and provide smoother turning.
To calculate the overall steering angle, you can use the following formula (First, people need to convert the steering angles from degrees to radians):
Two simplified versions:
(1)
(2)
The key difference between these formulas lies in how the distances between the front and rear axles (L) and between the front wheels (W) are incorporated.
In the first formula (1), the term appears in the numerator, while in the second formula (2), the term
appears. These terms determine the influence of the steering angles on the overall steering angle.
Formula (1) suggests that the impact of the steering angles on the overall steering angle is weighted more significantly, as it incorporates the ratio in the numerator. This indicates a stronger influence of the axle distance (L) on the overall steering angle.
Formula (2) assumes that the impact of the steering angles is relatively balanced, as it incorporates the ratio in the numerator. This implies that the wheelbase distance (L) and track width (W) have a relatively equal effect on the overall steering angle.
Therefore, the choice between the two formulas depends on the specific considerations and assumptions made regarding the influence of the distances between the front and rear axles and the front wheels on the overall steering angle.
Simplified assumption
The following models assume that the vehicle is turning on a flat surface. In real-world scenarios, factors like tire slip, suspension geometry, and uneven surfaces can affect the accuracy of these calculations.
When we only consider the steering angle delta, the longitudinal velocity , and the track width W to calculate the
. It assumes that the vehicle is moving on a flat surface, and the approximation is valid for small steering angles. However, it does not account for the Ackermann steering principle or the individual steering angles of the left (
) and right (
) wheels.
When we consider the average of the left, right steering angles, the longitudinal velocity , and the wheelbase distance L to calculate the
,. This expression assumes a symmetric steering setup and disregards the Ackermann steering principle.
Reference:
(1) https://link.springer.com/book/10.1007/978-0-387-74244-1 by Reza N. Jazar
(2) https://www.sae.org/publications/books/content/r-506/ by by Thomas D. Gillespie
(3) https://en.wikipedia.org/wiki/Ackermann_steering_geometry
(4) https://www.racecar-engineering.com/articles/tech-explained-ackermann-steering-geometry/
(5) Mobile Robot Kinematics - Autonomous Mobile Robots - ETH Zürich
(6) Mobile Robot Kinematics - CMU
(7) Modeling, Control and Path Planning for an Articulated Vehicle
(8) Tire model - Hans B. Pacejka
The calculation to derive the vehicle speed with the simplified models
Balanced car model (lateral two-wheel model)


Lateral two-wheels model
Longitudinal velocity:
Lateral velocity:
or
Bicycle model (longitudinal two-wheel model)

-20230516-132309.png?inst-v=e65987b7-7f92-4b87-8e0b-82ace1c12534)
Longitudinal two-wheels model
Longitudinal velocity:
or
whereis the rear wheel’s speed,
is the steering angle of the front wheel.
Lateral velocity:
or
In this case, the bicycle's speed can be calculated using a single wheel's angular speed (either front or rear) since they are assumed to be the same during normal conditions:
a bicycle's front and rear wheels can have different speeds, but this typically occurs under specific conditions, such as:
Skidding or slipping: When a bicycle skids or slips (e.g., on wet or icy surfaces), the rear wheel could lock up or lose traction, causing its speed to differ from the front wheel. In this case, the rear wheel speed could be lower than the front wheel speed.
Turning: During a turn, the front and rear wheels travel slightly different paths, and their speeds might differ momentarily. However, this difference is generally small and not as significant as in the case of skidding or slipping.
4WS vehicle model with all-steering (e.g., some tractors)

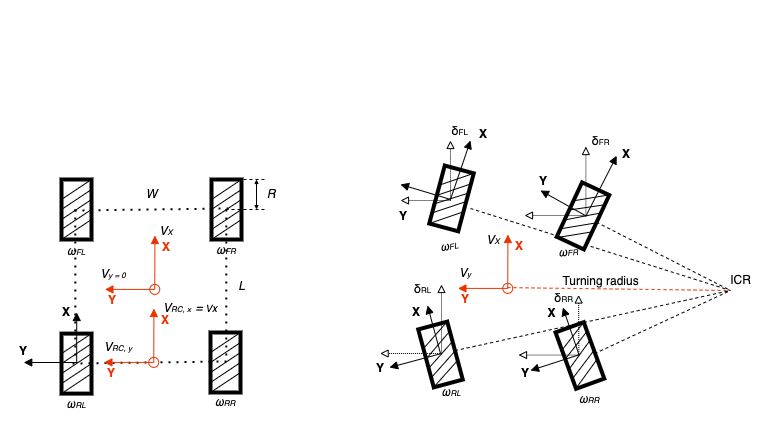
Four-wheel steering vehicle
Longitudinal velocity:
Lateral velocity:
in a simplified model, which the is already obtained.
4WS vehicle model with front steering

-20230526-131123.png?inst-v=e65987b7-7f92-4b87-8e0b-82ace1c12534)
vehicle model with front steering
Longitudinal velocity:
Lateral velocity:
or
FWD vehicle model with front steering

Longitudinal velocity:
Lateral velocity:
or
RWD vehicle model with front steering

Longitudinal velocity:
Lateral velocity:
or
RWD vehicle model with rear steering (e.g., large sweeper)

Longitudinal velocity:
Lateral velocity:
or
4WS vehicle model without a steering wheel (e.g., some robotic chassis)

For a 4WS vehicle model without a steering wheel (e.g., some robotic chassis), the steering is typically controlled by differential wheel speeds.
Longitudinal velocity:
Lateral velocity:
Front-rear axle articulated vehicle (front steering, e.g., some tractors)
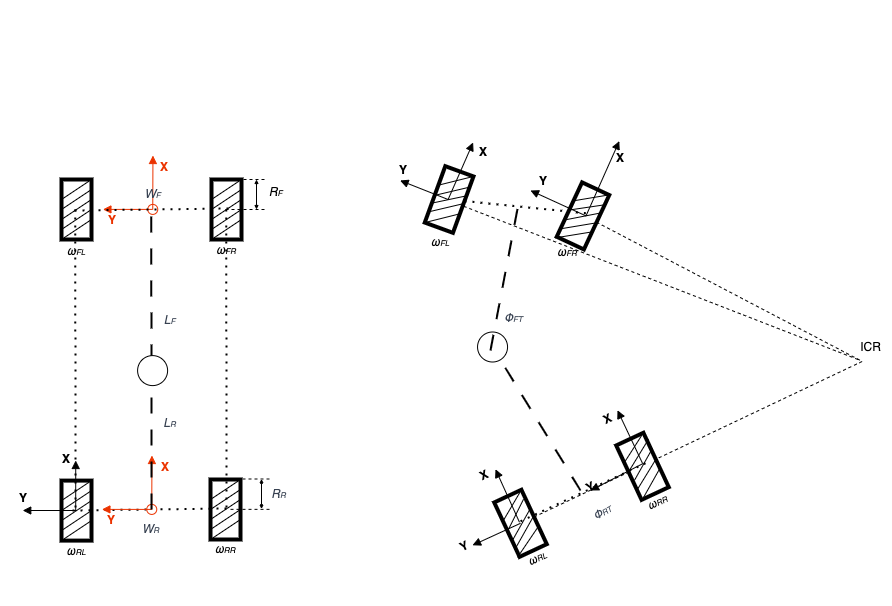
Front-rear axle articulated vehicle
Longitudinal velocity:
Lateral velocity:
In these equations:
represent the radii of the front and rear wheels
represent the lengths of the front and rear segments
represent the transaxle rotational rate of the front and rear segments
represent the track widths of the front and rear segments
Example of the calculation accuracy when using different models
The example code
About OBD2
While OBD2 (On-Board Diagnostics 2) is a widely used standard for vehicle diagnostics and monitoring, it does have limitations when it comes to using it as a sensor fusion wheel speed resource, particularly in terms of resolution. Here are some limitations of OBD2 in this context:
Limited Resolution: As you mentioned, the OBD2 standard typically provides wheel speed information with a 1 km/h resolution. This limited resolution may not be sufficient for applications that require more precise and accurate measurements, such as advanced driver assistance systems (ADAS) or autonomous driving. In the low-velocity dynamic scenarios, it would not be accurate for the robotic to do the localization as the motion estimation system relying on wheel speed will think the robot is static when the speed is below 1km/h.
Sampling Rate: OBD2 is not designed to provide real-time data, and the wheel speed information sampling rate can be relatively slow. The standard refresh rate for OBD2 data is generally around 1-5 seconds. This delay in data acquisition and transmission may not be suitable for time-critical applications that require faster response times.
Dependence on Vehicle Systems: OBD2 relies on the functionality and accuracy of the vehicle's onboard systems, particularly the ABS. If the ABS sensors are faulty or not calibrated correctly, the wheel speed data obtained through OBD2 may not be reliable. This dependency on the vehicle's systems can limit the overall accuracy and performance of the wheel speed measurements.
Compatibility and Standardization: While OBD2 is a widely adopted standard, there can still be variations in implementation across different vehicle manufacturers and models. This lack of standardization can affect the consistency and compatibility of wheel speed data obtained through OBD2, making it challenging to rely on it as the sole source for sensor fusion applications.
We strongly recommend that our customers consider acquiring higher-resolution wheel speed signal resources or utilize the direct velocity estimation method to stream into the VRTK2 fusion engine.
